
Los números
reales son los números que se puede escribir con anotación decimal,
incluyendo aquellos que necesitan una expansión decimal infinita. El conjunto
de los números reales contiene todos los números enteros, positivos y
negativos; todas las fracciones; y todos los números irracionales, aquellos
cuyos desarrollos en decimales nunca se repiten.
Subconjunto de
los números Reales
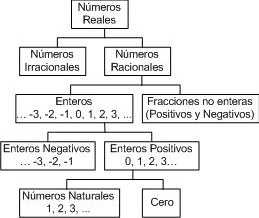
Propiedades y operaciones
con los números reales
Dos números, en
la recta numérica, que están a la misma distancia del cero pero en direcciones
opuestas se denominan:
Inversos
aditivos, opuestos o simétricos uno del otro. Por ejemplo:
3 es el inverso
aditivo de -3, y -3 es el inverso aditivo de 3
El numero 0
(cero) es su propio inverso aditivo.
La suma de un
número y su inverso aditivo es 0 (cero).
Inverso
aditivo
Para cualquier
número real de a, su inverso aditivo es –a.
Considere el
número -4. Su inverso aditivo es -(-4). Como sabemos que este número debe ser
positivo, esto implica que -(-4) = 4. Éste es un ejemplo de la propiedad del doble negativo.
Propiedad del
doble negativo
Para cualquier
número real a, -(-a) = a
Por la propiedad
del doble negativo, -(-6.9) = 6.9
Valor absoluto
El valor de cualquier número distinto del cero siempre
será un numero positivo, y el valor absoluto de 0 es 0.
Para determinar
el valor absoluto de un número real, use la definición siguiente.
La definición de
valor absoluto indica que el valor absoluto de cualquier número no negativo, es
el mismo, y el valor absoluto de cualquier número negativo es el inverso
aditivo (opuesto) del número.
El valor absoluto
de un número puede determinarse por medio de la definición. Por ejemplo.
1. Sumar
números reales
2. Restar números
reales
3. Multiplicar números reales
4. Dividir números reales
3. Multiplicar números reales
4. Dividir números reales
INTEGRANTES:
ROSALIA RIVERA
LUIS CARLOS DIAZ
SHAREN VARGAS
ROSALIA RIVERA
LUIS CARLOS DIAZ
SHAREN VARGAS
Multiplicar números reales
ResponderEliminarPara multiplicar dos números con signos iguales, ambos positivos o ambos negativos, multiplique sus valores absolutos. La respuesta es positiva.
Para multiplicar dos números con signos diferentes, uno positivo y el otro negativo, multiplique sus valores absolutos. La respuesta es negativa.
Cuando multiplicamos más de dos números, el producto será negativo cuando exista un número impar de números negativos. El producto será positivo cuando exista un número par de números negativos.
Propiedad del cero en la multiplicación
Si a, b, c son números reales, se verifican las siguientes propiedades:
ResponderEliminarS1- ASOCIATIVIDAD DE LA SUMA: (a+b)+c = a+(b+c)
S2- CONMUTATIVIDAD DE LA SUMA: a+b = b+a
S3- 0 ES NEUTRO ADITIVO, o sea: a + 0 = a , para todo a∈ IR..
S4- TODO NÚMERO REAL TIENE INVERSO ADITIVO, esto es: dado a∈IR,
existe un único número real, que notaremos con −a, tal que a+(-a) = 0
M1- ASOCIATIVIDAD DEL PRODUCTO: (a.b).c = a.(b.c)
M2- CONMUTATIVIDAD DEL PRODUCTO: a.b = b.a
M3- 1 ES NEUTRO MULTIPLICATIVO, o sea: 1.a = a , para todo a∈IR..
M4- TODO NÚMERO REAL DISTINTO DE 0 TIENE INVERSO MULTIPLICATIVO, esto es: dado a∈IR, a ≠ 0, existe un único número real, que notaremos con 1/a, tal que a.1/a = 1
D- DISTRIBUTIVIDAD DEL PRODUCTO CON RESPECTO A LA SUMA: a.(b+c) = a.b+a.c
El sistema de los numeros reales no esta circunscrito sólo al conjunto IR, sino constituye un sistema donde, además del conjunto IR, hay dos operaciones, una relación de igualdad y una relación de orden que satisfacen un conjunto de axiomas....
ResponderEliminaraxiomas de orden
tricotomia : si a,b e IR,entonces se verifica una de las siguientes relaciones :
a<b ó a=b ó b<a
Nota:
ResponderEliminarLos números reales se expresan con fracciones decimales que tienen una secuencia infinita de dígitos a la derecha de la coma decimal, como por ejemplo 324,8232. Frecuentemente también se sobre presentan con tres puntos consecutivos al final (324,823211247…), lo que significaría que aún faltan más dígitos decimales, pero que se consideran sin importancia.
Nota:
ResponderEliminarLos números reales se expresan con fracciones decimales que tienen una secuencia infinita de dígitos a la derecha de la coma decimal, como por ejemplo 324,8232. Frecuentemente también se sobre presentan con tres puntos consecutivos al final (324,823211247…), lo que significaría que aún faltan más dígitos decimales, pero que se consideran sin importancia.
Nota:
ResponderEliminarLos números reales se expresan con fracciones decimales que tienen una secuencia infinita de dígitos a la derecha de la coma decimal, como por ejemplo 324,8232. Frecuentemente también se sobre presentan con tres puntos consecutivos al final (324,823211247…), lo que significaría que aún faltan más dígitos decimales, pero que se consideran sin importancia.