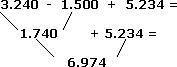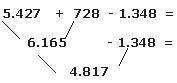Conjuntos

Conjunto. Colección de objetos sin repetición donde el orden de éstos no importa.

Un conjunto queda perfectamente definido si se conocen con exactitud los elementos que lo integran o que pertenecen a él; es decir, si se nombran todos sus elementos o bien si se usa un enunciado o propiedad que lo identifique. Independientemente de la forma en que se lo represente, siempre se usa una letra mayúscula que lo define. Esta letra mayúscula representa a un conjunto específico de elementos.

Notación de conjuntos

Se utilizarán las letras mayúsculas, tales como A, B y C para nombrar conjuntos. Por  ejemplo:

Es bastante corriente dibujar los conjuntos esquemáticamente, una simple curva cerrada representa el conjunto y en su interior se disponen todos los elementos que pertenecen a él. A estos esquemas se les denomina diagramas de Venn.

A cada objeto de un conjunto se le llama elemento de él. Se dice que dicho elemento pertenece al conjunto. Simbólicamente:

Conjunto Vacío

Un conjunto que carece de elementos se llama conjunto vacío. Pero, ¿existen conjuntos vacíos?. ¿Cómo se podrían determinar? Consideremos el conjunto A formado por todos los triángulos de cuatro lados. ¿Está bien determinado?. ¡Sí! : Podemos saber exactamente si un objeto le pertenece o no. Sabemos que ningún triángulo tiene cuatro lados. Por lo tanto este conjunto no tiene ningún elemento. Es un ejemplo de conjunto vacío.

El conjunto B de los números “x” que cumplen : x + 5 = x + 3 , ¿es un conjunto vacío? Sí, porque no existe un número que cumpla esa condición.

Formas de determinar un conjunto

Ya hemos visto dos formas de determinación de conjuntos. Una forma gráfica (llamada: diagramas de Venn) y otra listando todos sus elementos entre corchetes (llamada: por extensión).

Veamos algunos inconvenientes de estas formas. Si un conjunto tiene 4789 elementos, su representación por diagramas o extensión es posible, pero poco práctica. Peor aún, si el conjunto que se quiere determinar es infinito, su representación no sería posible. Existe una tercer forma denominada “por comprensión” que es especialmente adecuada para representar conjuntos infinitos.

¿Qué significa determinar un conjunto por comprensión?

Por ejemplo, el conjunto {números pares} está bien determinado porque podemos decidir si un número pertenece o no a él; y además es un conjunto infinito. No se nombran uno a uno sus elementos sino que se da una propiedad común a todos ellos y a ningún otro. Esto es representar un conjunto por comprensión. Hasta ahora se han proporcionado unos pocos ejemplos. ¿En cuál de los ejemplos anteriores, el conjunto está determinado por comprensión?

Notación para conjuntos determinados por comprensión

Igualdad de Conjuntos

Diremos que dos conjuntos son iguales si tienen los mismos elementos. Es decir, A=B , sí y sólo si todo elemento de A pertenece a B y todo elemento de B pertenece a A.

Consecuencias de la definición de igualdad de conjuntos son: 

• Si A = B , las letras A y B son nombres distintos para el mismo conjunto.
• Existe un único conjunto vacío.
• Los conjuntos (a , b , c) , (a , a , b , b , c , c) y (a , a , c , b , a , c) son él mismo conjunto. (Los tres tienen los mismos elementos. Por lo tanto no es útil repetir elementos en la escritura por extensión y tampoco es importante el orden en que se escriben).

Inclusión de Conjuntos

Considere el siguiente ejemplo:

Todos los elementos de A son también elementos del conjunto B. Diremos que A está incluido en B. También decimos que A es subconjunto o parte de B. En este caso en particular estamos hablando de inclusión estricta.

Operaciones de Conjuntos

En aritmética se estudian operaciones entre números, (Adición, Sustracción, etc.). La operación numérica de sumar hace corresponder a cada par de números, a, b, un nuevo número (a+b) que es su suma (resultado de la operación de sumar). También es posible operar con conjuntos. En este caso, el resultado de operar dos conjuntos será un nuevo conjunto. Definiremos algunas de las operaciones posibles: Unión, Intersección, Diferencia, Complemento, Diferencia Simétrica y Producto Cartesiano.

Un elemento pertenece a la unión de A y B si está en A o si está en B. Es decir, es suficiente que sea elemento de alguno de los dos.

Se llama intersección de dos conjuntos A y B (y se anota A B) al conjunto cuyos elementos son los que pertenecen a la vez a A y a B.

Integrantes:

Sharen Vargas.

Rosalía Rivera.

Luis Carlos Díaz.

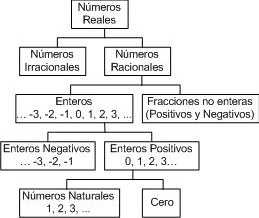
NÚMEROS REALES

                   

Los números reales son los números que se puede escribir con anotación decimal, incluyendo aquellos que necesitan una expansión decimal infinita. El conjunto de los números reales contiene todos los números enteros, positivos y negativos; todas las fracciones; y todos los números irracionales, aquellos cuyos desarrollos en decimales nunca se repiten.

Subconjunto de los números Reales

                                                        

Propiedades y operaciones con los números reales

Dos números, en la recta numérica, que están a la misma distancia del cero pero en direcciones opuestas se denominan:

Inversos aditivos, opuestos o simétricos uno del otro. Por ejemplo:

3 es el inverso aditivo de -3, y -3 es el inverso aditivo de 3

El numero 0 (cero) es su propio inverso aditivo.

La suma de un número y su inverso aditivo es 0 (cero).

Inverso aditivo

Para cualquier número real de a, su inverso aditivo es –a.

Considere el número -4. Su inverso aditivo es -(-4). Como sabemos que este número debe ser positivo, esto implica que -(-4) = 4. Éste es un ejemplo de la propiedad del doble negativo.

Propiedad del doble negativo

Para cualquier número real a, -(-a) = a

Por la propiedad del doble negativo, -(-6.9) = 6.9

Valor absoluto

El valor de cualquier número distinto del cero siempre será un numero positivo, y el valor absoluto de 0 es 0.

Para determinar el valor absoluto de un número real, use la definición siguiente.

La definición de valor absoluto indica que el valor absoluto de cualquier número no negativo, es el mismo, y el valor absoluto de cualquier número negativo es el inverso aditivo (opuesto) del número.

El valor absoluto de un número puede determinarse por medio de la definición. Por ejemplo.

Operaciones con los números Reales

1. Sumar números reales

2. Restar números reales
3. Multiplicar números reales
4. Dividir números reales

INTEGRANTES:

ROSALIA RIVERA
LUIS CARLOS DIAZ
SHAREN VARGAS

Operaciones combinadas

Las operaciones combinadas son aquellas en las que aparecen varias operaciones aritméticas para resolver. Para obtener el resultado correcto deben seguirse las siguientes reglas: - Se resuelven las operaciones encerradas entre paréntesis, corchetes y llaves en el   siguiente orden: 1) Potenciación y radicación                               2) Multiplicación y división                               3) Suma y resta - Se resuelven las sumas y las restas que separan los términos.

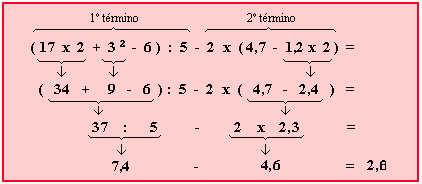
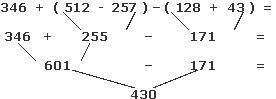
Operaciones combinadas.

Es una expresión formada por números en operaciones diversas y agrupados de formas diversas mediante paréntesis, corchetes y llaves. Para resolver operaciones combinadas debemos dominar todo lo estudiado anteriormente.

- La misión de los paréntesis es la de unir o "empaquetar" aquello a lo que afectan. - Los signos de multiplicar unen más que los de sumar y restar, es decir, cuando dos números están unidos por el signo de multiplicar forman un bloque inseparable, mientras que si los une un signo de sumar o restar están más sueltos. - Debemos conocer las propiedades de las operaciones para no hacer algo que sea incorrecto. - Para poder sumar o restar dos números deben estar sueltos, no podemos sumar dos números si uno de ellos está unido por el otro lado a otra expresión mediante un signo de multiplicar. - Las operaciones combinadas se resuelven en varios pasos, todo lo que no se resuelva en un paso se debe copiar otra vez tal como estaba, sin olvidarlo ni cambiarlo de posición. - Por eso, antes de comenzar a resolver operaciones combinadas debemos observar la expresión y plantearnos una estrategia a seguir, lo que vamos a hacer antes y después. - Como norma general es aconsejable comenzar resolviendo lo del interior de paréntesis, seguir luego con las multiplicaciones y terminar realizando las sumas que queden. Hemos revisado cada una de las operaciones matemáticas: adición, sustracción, multiplicación y división. Conocimos los elementos que tiene cada operación: Sumandos y suma de la adición. Minuendo, sustraendo y resta o diferencia para la sustracción. Factores y producto, de la multiplicación Dividendo, divisor y cuociente; y el resto, que aparece cuando no es exacta, de la división. Identificamos a la sustracción como operación inversa de la adición y a la división, como la inversa de la multiplicación. Muchas veces las operaciones van combinadas, es decir, hay 2 o más operaciones juntas y se deben resolver todas para obtener el resultado final. Adición y sustracción Si un ejercicio presenta adición y sustracción, debemos resolver las operaciones en el orden que se presentan, comenzando desde la izquierda. Un ejemplo: Como la sustracción va primero, obtenemos la resta, que en este caso es 1740. Luego , la anotamos debajo y, después, le sumamos los 5.234. El resultado final es 6.974. En el caso que la adición estuviera en primer lugar, quedaría: Primero resolvemos la adición , y a la suma obtenida le restamos 1.348. El resultado final es 4.817 Un signo especial Hay un signo muy utilizado que nos señala las operaciones que se deben hacer primero; lo conocemos como paréntesis ( ) . Cuando hay paréntesis, los debemos resolver en primer lugar. Analicemos el siguiente ejemplo: Como puedes ver, los paréntesis se resuelven en el orden que aparecen de izquierda a derecha. Se pone el resultado de las operaciones, que van dentro de ellos, debajo de cada uno. Luego, se obtiene la suma que está a la izquierda. Para terminar, restamos su resultado con el número final.

Operaciones combinadas

Para resolver operaciones combinadas (suma, resta, multiplicación y división) seguimos 

un orden establecido. Se llama jerarquía de operaciones. 

   -ƒ Primero se realizan las operaciones entre paréntesis. 

ƒ   - Después las multiplicaciones y divisiones. 

   - Por último las sumas y restas. 

ƒ Cuando las operaciones tienen el mismo rango, se realizan de izquierda a derecha. 

              (3 + 5) x 4 – 7 x (15 – 11) = 8 x 4 – 7 x 4 = 32 – 28 = 4 

                           8 x 4 – 7 x 4 = 

                              32 – 28 = 4 

Ejemplos:

· 9 + (6 + 5 – 3) – 12 : 4 =

9 + (6 + 5 – 3) – 12 : 4 = 27 + 8 – 3 = 32

 2 + 5 · (2 ·3)³ =   2 + 5 · (2 ·3)³ = 2 + 5 · (6)³ = 2 + 5 · 216 = 2 + 1080 = 1082

 440 − [30 + 6 (19 − 12)] =   440 − [30 + 6 (19 − 12)] = 440 − (30 + 6 · 7)] = 440 − (30 + 42) =     = 440 − (72) = 368

 2{4[7 + 4 (5 · 3 − 9)] − 3 (40 − 8)} =  = 2{4[7 + 4 (15 − 9)] − 3 (40 − 8)}=    = 2[4 (7 + 4 · 6) − 3 (32)] = 2[4 (7 + 24) − 3 (32)]=       2[4 (31) − 3 (32)]= 2 (124 − 96)= 2 (28)= 56

INTEGRANTES:

ROSALIA RIVERA

LUIS CARLOS DIAZ

SHAREN VARGAS

Ejercicio sobre proposición compuesta

“Si tuvieran que justificarse ciertos hechos por su enorme tradición entonces, si 
estos hechos son inofensivos y respetan a todo ser viviente y al medio ambiente, no 
habría ningún problema. Pero si los hechos son bárbaros o no respetuosos con los 
seres vivientes o el medio ambiente, entonces habría que dejar de justificarlos o no 
podríamos considerarnos dignos de nuestro tiempo.”

Formalización:

p → [ ( q ˄ r ˄ s) → ¬t ] ˄ [ (¬q ˅ ¬( r ˅ s ) → ( ¬p ˅ ¬u ) ]

Ejemplo Prop. Compuesta

Es falso que Ana no juega voley ni fútbol, por lo tanto podrá estar en el equipo de voley o en el de fútbol, si y solo si entrene demasiado porque son equipos superiores.

El Enunciado

Un enunciado es un acto de habla (acto locativo) mínimo, normalmente realizado mediante una oración o una expresión sintáctica más pequeña que una oración. Informalmente se usa enunciado como sinónimo de oración, aunque pragmáticamente existen diferencias. Por ejemplo, una misma oración dicha en diferentes contextos corresponde a enunciados diferentes. Y viceversa, diferentes oraciones pueden realizar o concretar un mismo enunciado:

Quiero que saques la basura.

¿Puedes sacar la basura?

Saca la basura, por favor.

¿Quieres sacar la basura?

                                                                                         

La Proposición

Es un producto lógico del pensamiento que se expresa mediante el lenguaje, sea éste un lenguaje común o formalizado, cuando adopta la forma de oración gramatical, o simbólico, cuando se expresa por medio de signos o símbolos de un lenguaje formal.

En Lógica tradicional se distinguen la proposición y el juicio, por cuanto la primera es el producto lógico del acto por el cual se afirma o se niega algo de algo, mientras ese acto constituye el juicio.

Se clasifica en:

Proposición Simple: En matemáticas, una proposición simple es un enunciado del cual se puede afirmar que es verdadero o que es falso pero no ambos a la vez.

Ejemplos: 
-La caja de madera
-Está lloviendo

Proposición Compuesta:Las proposiciones compuestas son aquellas que se forman por unión de proposiciones simples mediante los conectivos lógicos.

Ejemplo:

 La caja es de madera y está lloviendo

Lógica

La lógica es una ciencia formal que estudia los principios de la demostración e inferencia válida. La lógica es la inferencia. La inferencia es el proceso por el cual se derivan conclusiones a partir de premisas. La lógica investiga los principios por los cuales algunas inferencias son aceptables, y otras no. Cuando una inferencia es aceptable, lo es por su estructura lógica, y no por el contenido específico del argumento o el lenguaje utilizado. Por esta razón la lógica se considera una ciencia formal, como la matemática, en vez de una ciencia empírica.

La lógica tradicionalmente se consideró una rama de la filosofía.